Objective 1: Exploring the four subspaces of quasi-Toeplitz data matrices
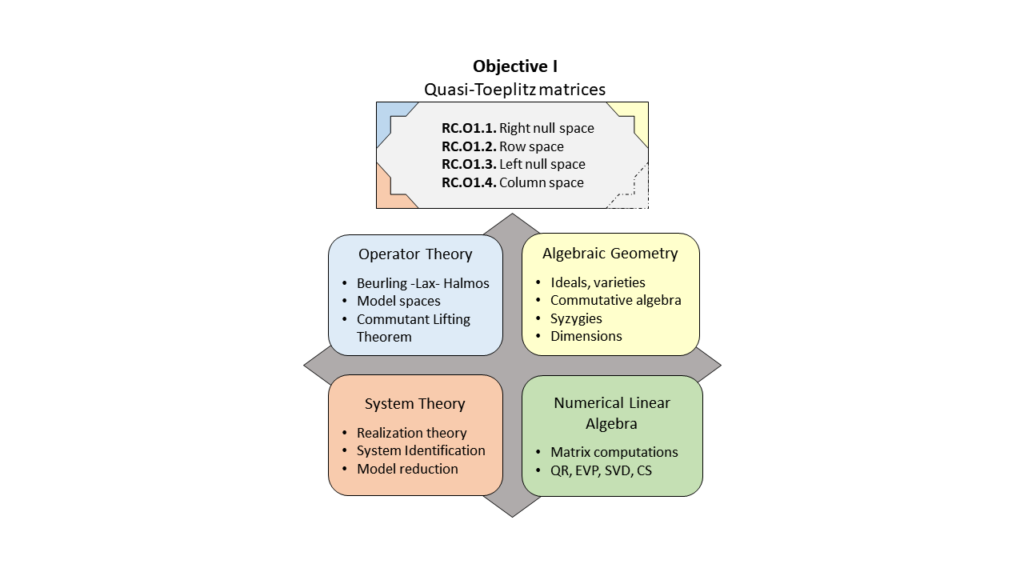
In Objective 1, we pinpoint and exploit important correspondences between operator theory, algebraic geometry and our research. We will study the rich structure of quasi-Toeplitz data matrices by looking at their four fundamental subspaces: their right null space, their row space, their left null space and their column space.
Challenge 1:
The right null space of the quasi Toeplitz matrices
- Prove that the null space of the each of the quasi-Toeplitz matrices is a scalar or vector, single- or multi-shift invariant projective subspace
- Generalization of the Weierstrass canonical form for more than two matrices to characterize the right null space
Challenge 2:
The row space of the quasi-Toeplitz matrices
The row space of the quasi-Toeplitz matrices is the counterpart of the ideal in algebraic geometry and of the forward shift invariant subspace of operator theory.
- Assess the multi-shift invariant structure of the row space
- Derive an appropriate generalization of the theorem of Cayley-Hamilton for multidimensional commuting systems to show the connection between the row space and nD difference equations
- Give an interpretation to the Buchberger algorithm in our numerical linear algebra framework
Challenge 3:
The left null space of the quasi-Toeplitz matrices
The left null space corresponds in algebraic geometry to the module of 1st order syzygies. The challenge is to translate important notions of Hilbert functions and Hilbert’s syzygy theorem to our vector space approach.
Challenge 4:
The column space of the quasi-Toeplitz matrices
Due to the duality between the column space of the quasi-Toeplitz matrices and their right null space, we can interpret the algorithms designed for the null space in the column space.
- We postulate that by applying Grassmann’s dimension theorem, we will be able to determine the number of affine roots directly from the column space, so that the explicit calculation of the right null space, followed by several rank tests, is not needed.
- If true, this may evolve in a data-driven polynomial rooting algorithm and numerical linear algebra algorithms for elimination of variables.